筑波小のペーパー課題「重ね図形」「回転図形」などの「点図形」形式の課題の解き方のコツ。

三連休のお教室が、無事に終了いたしました。
本日までの三連休、
金曜日の「オールインワン講座」
土曜日の「筑波対策 図形課題集中特訓」と「絵画制作講習」
本日の「国立小受験 専門 定期教室」
と、連日のお教室、講習会となっておりました。
ご参加の皆様、
この連休も、真剣にお勉強に取り組み、
有意義な学びの時間を一緒に創ってくださり、ありがとうございます。
ご家庭で継続してきた「頑張り」の成果が、明らかです。
まだまだ、形としては見えてきていない「頑張り」は、もっともっと沢山あることでしょう。
今の、学習に向けた取り組み、
うまくいかない時も、お子さまと一緒に、ねばり強く課題に向き合ってきたお母さま、お父さまの姿勢は、
将来に向けた学びの土台になっています。
今のお勉強の「効果」は、小学校受験そのものだけにとどまりません。
2年後、5年後、10年後。
今から、楽しみにしていてください。
重ね図形、回転図形の「点図形」形式の問題の解き方のコツについて、ご紹介します。
昨日の、「筑波小対策 図形課題集中特訓」を受けてのご質問にもありました、
「点図形」の問題の解き方のコツを、ご紹介します。
点図形の「コツ」は、明快です。
それは「始点」と「終点」を意識することです。
例えば、純粋な「点図形」の問題を例にとって考えてみましょう。
問)左のお部屋の形と同じになるように、右の点を結んでください。
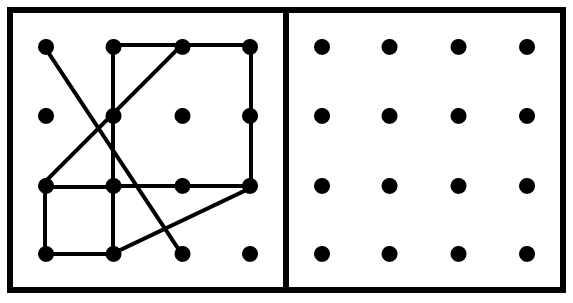
このような「同じように書き写す」問題でも、初めは難しいかもしれません。
例えば、この形の中の1本の線(赤色の線)について考えてみましょう。
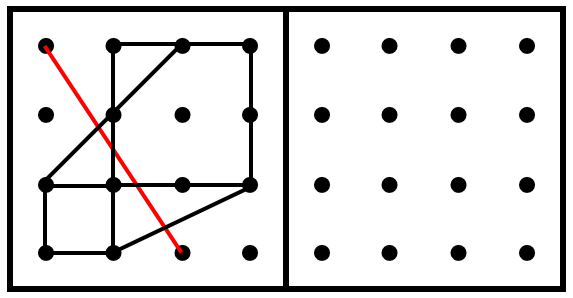
「縦の線」「横の線」と比べると、「斜めの線」は難易度が上がります。
なぜならば、線を「〇〇」の方向に向かって書いていく、という考え方で、点図形の問題に取り組む場合が多いからです。
縦の線なら「下」に、横の線なら「右」に線を書いていけば、問題ありません、
ところが、この右斜め下に伸びる線の場合、少し困ったことが起こります。
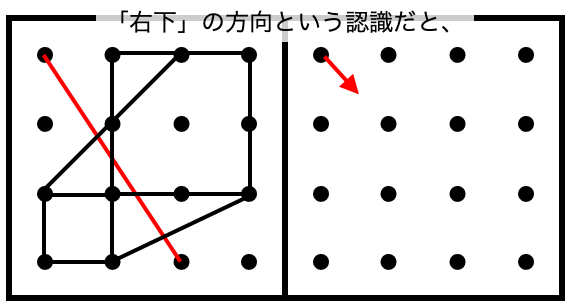
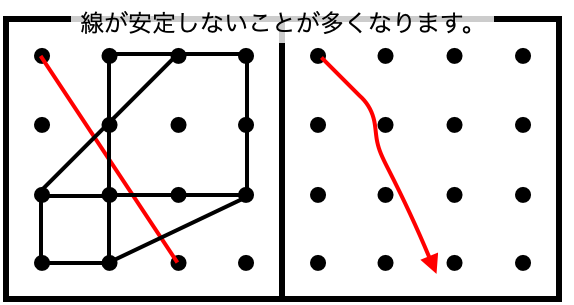
目的とする点まで、正しく線を書くことができない、という場合も、珍しくはありません。
そこで、「始点」と「終点」を意識する考え方の登場です。
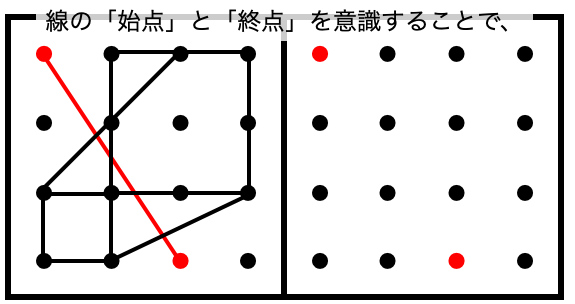
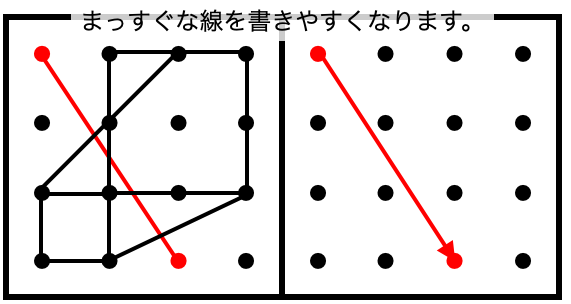
点図形の問題について、まずは、
「始点」と「終点」を意識して、正しく書き写すことができているか、から、確かめるようにしてください。
この段階を一足飛びにして、重ね図形や回転図形に取り組もうとしても、
なかなかうまくいかないことも多いでしょう。
その上で、「重ね図形」「回転図形」の解き方のコツをみていきます。
「重ね図形(折り重ね)」:始点と終点について「近くは近く」「遠くは遠く」
横にずらして重ねる重ね図形については、
先ほどの「同じように書き写す」ができれば問題なく解けるので、ここではその説明は割愛します。
ここでは、真ん中の線で折って重ねる場合の重ね図形(ひっくり返したり裏返したりする「反転」や、鏡に映すなどの「線対称」系の問題を含む)について考えていきます。
問)真ん中の太い線で折ったときに、左の線がぴったり重なるように、右側のお部屋の点と点を赤のクーピーで結んでください。
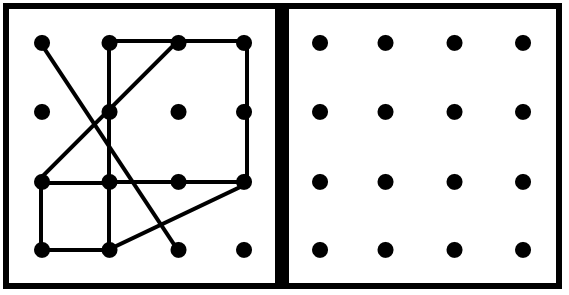
今回も、同様に、先ほどの例と同じ直線について考えていきましょう。
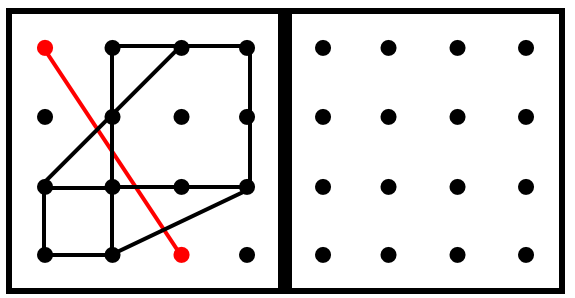
この直線の「始点」と「終点」を考えると、右側の赤で示した点となります。
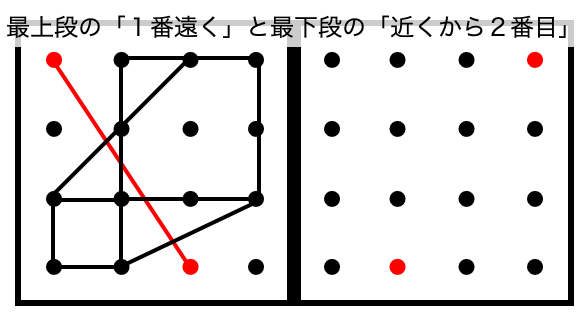
折り重ねる重ね図形については、
「近くは近く」「遠くは遠く」を合言葉にして考えるのがポイントです。
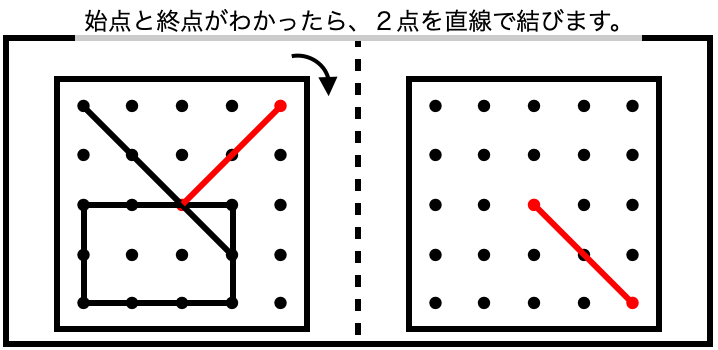
始点と終点が分かれば、
あとは、始点から終点に向かって線を引くだけです。
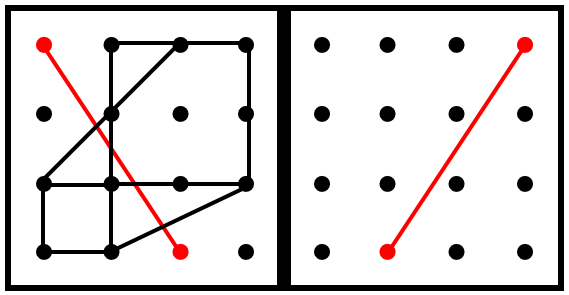
上記の点図形については、「マス」単位で考えることもできます。
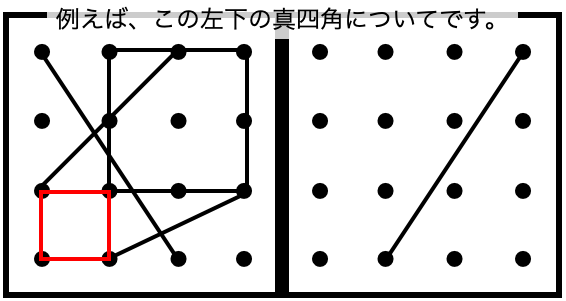
これも「一番下の『遠く』」と認識できれば、
一気に、形を書くことができるはずです。
同様に、
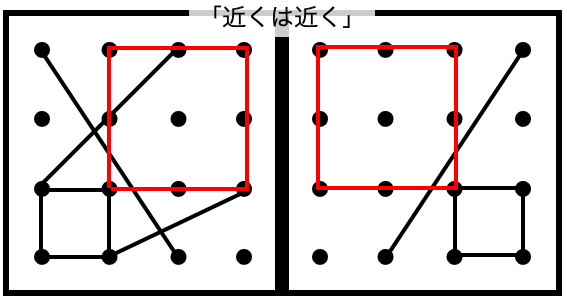
こちらの形も、同じようにひとつの「まとまり」として考えることができますね。
回転図形(回転位置移動):始点・終点を「右(左)に○回まわす」
今度は、回転図形についてみていきます。
昨日の筑波講習でも出題した、この問題を例に考えていきましょう。
問)左の形を右に1回だけ回した時の形を、右のお部屋に赤のクーピーで書いてください。
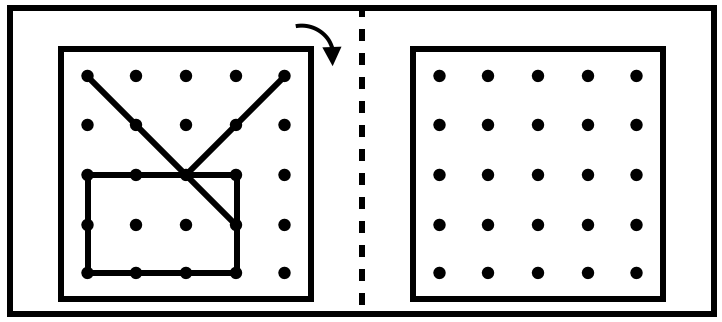
まずは、この直線について考えていきましょう。
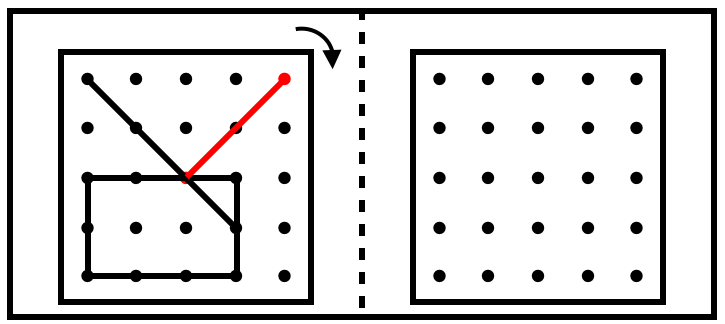
始点と終点は、「真ん中の点」と「右上の点」ですから、
「右に1回」だけ回ったとき、
・「真ん中の点」は移動しないため「真ん中」のまま
で、
・「右上の点」は「右下」に来ることがわかります。
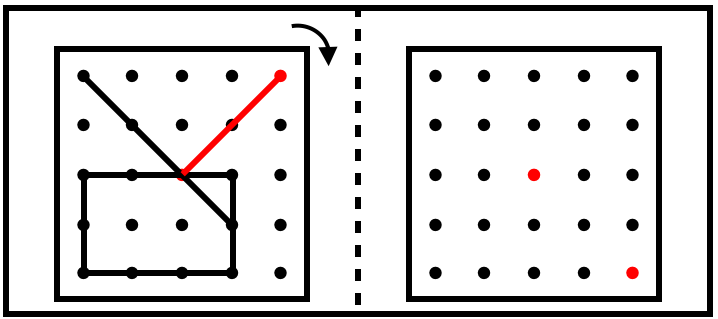
あとは、これまでと一緒です。
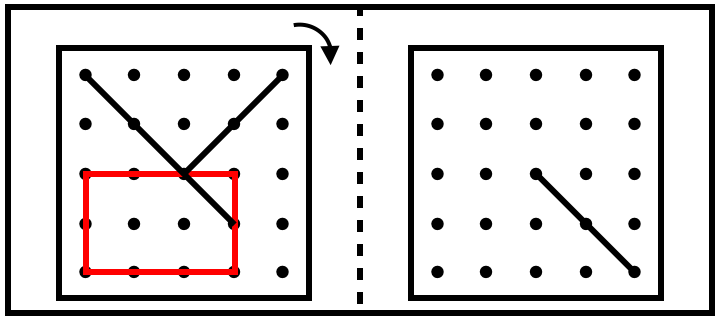
回転図形でも、「ひとまとまりの形」として考えることは有効です。
例えば、この「長四角も」、
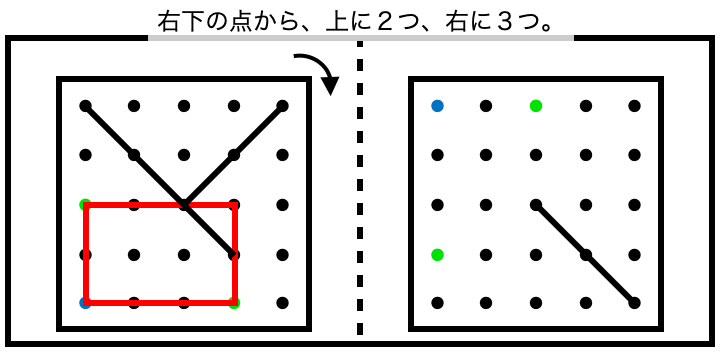
このように、それぞれの対応する頂点の位置を見つけられれば、
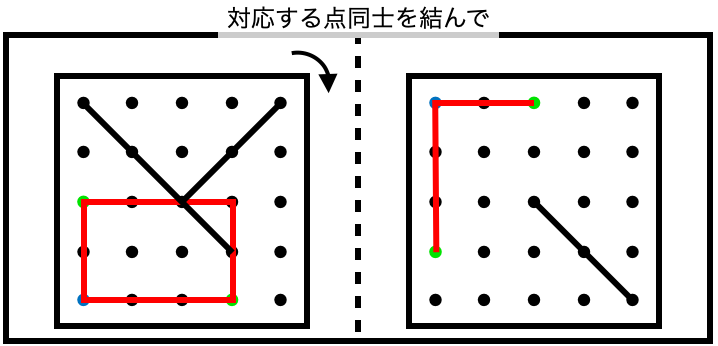
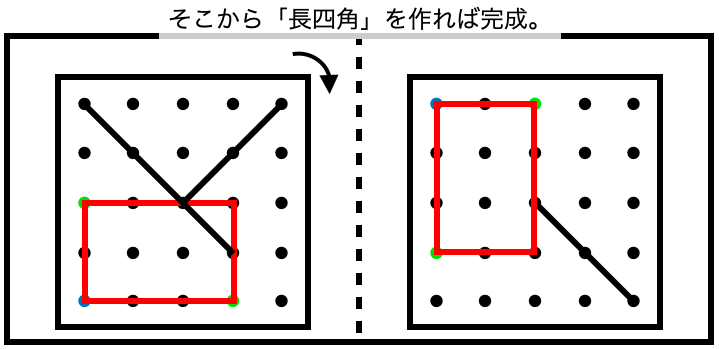
最後の1本の直線も、
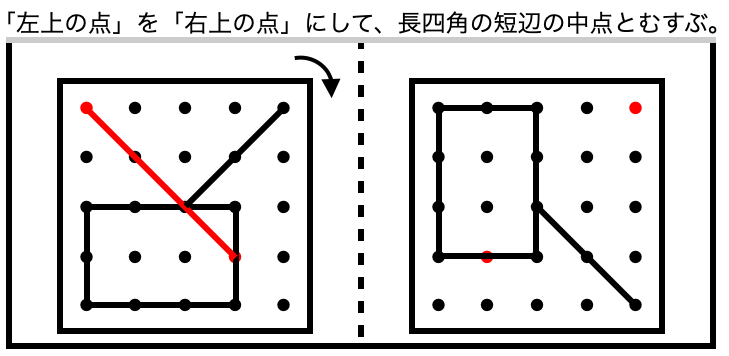
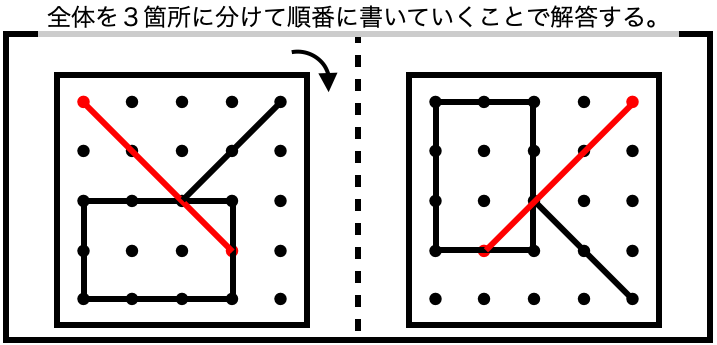
こうすることで、スムーズに答えを書くことができるようになります。
あわせて読みたい
まずは、基本的な「解き方の手順」を理解しましょう。
やり方を理解したら、あとは「練習あるのみ」です。
実際に解答をするときは、
ひとつひとつを言語化しているわけではなく、同じような思考を高速で行いながら、
ためらいなく線を書いていくことになります。
これには、「慣れ」による技術の向上も必要になってきます。
ペーパー課題も、ある種の運動競技だと言っても良いでしょう。
逆に言えば、
理屈を理解することができたら、
あとは、繰り返し練習をすることで、どんどんスピードアップしていけるのが、ペーパー課題の特徴でもあります。
まずは、基本の考え方を理解して、
そこから、繰り返し手を動かして「スピード」を身につけていきましょう。
同じペーパーの問題も、
何度も取り組んで、「自己最高記録」の更新を目指してください。
ゲーム感覚で、楽しみながらペーパー課題に取り組んでいき、
いつの間にか、ペーパー課題を「得意科目」へと変えていきましょう。