小学生からの算数学習にもつながる。「数の構成」についてゲーム感覚で理解を深めましょう。

今回は、小学校受験のペーパー課題の中のひとつ「数の構成」について取り上げます。
小学校受験における「数の構成」の問題を、どのように学習していけばよいか見ていきましょう。
例題)5個のリンゴをイヌさんとウサギさんで余らせないように分けました。空いているお皿にはリンゴはいくつになるでしょうか。赤のクーピーで○(まる)をつけてください。
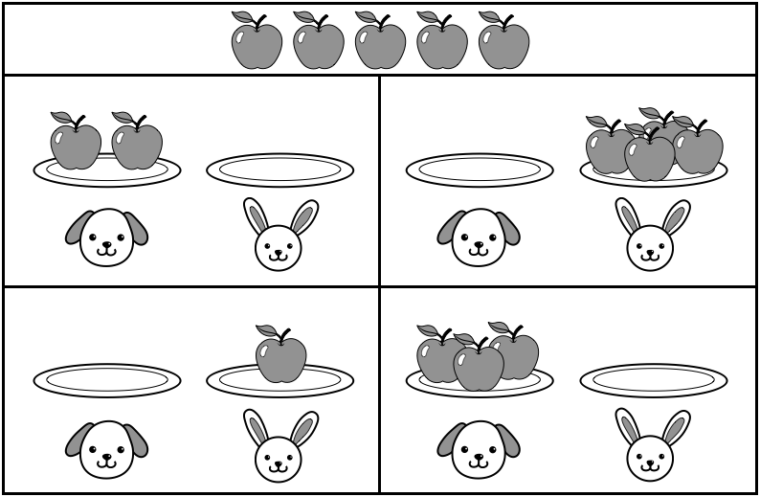
このような問題を「数の構成」の問題と呼んでいます。
今回は、「5個のリンゴ」を「いくつといくつに分けることができるか」ということなので、
「5の構成」の問題です。
この例題を使って、「数の構成」の問題の解き方・学習法を説明していきます。
ステップ1:全部で○個になるまで、解答欄に形を書く。
例えば、例題の左上のお部屋の問題について見てみると、
左側の「イヌさん」のお皿には、リンゴが2個あります。

なので、右側の「ウサギさん」のお皿に、3個目、4個目、5個目のリンゴが入るように、「○」を書き足していきます。
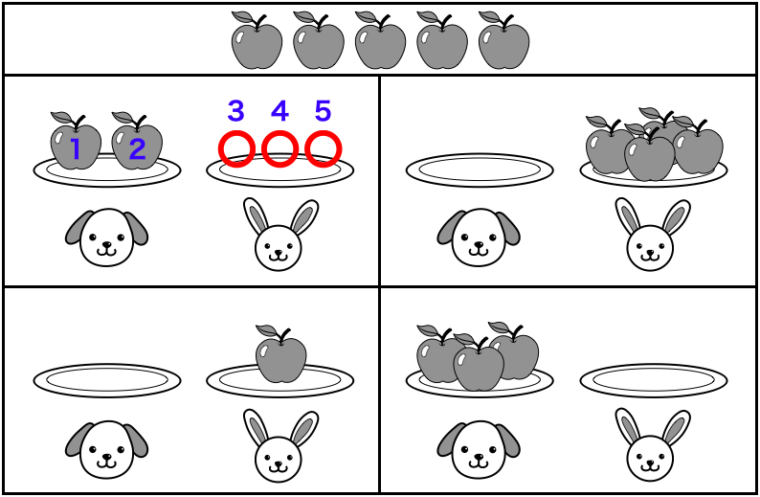
※注)青色で書いてある数字は、ペーパーで解答をする際に書き込むものではなく、心の中で数え上げる時の数を表示しています。
この「ステップ1」のやり方では、
「全部でいくつになるか」を把握していて、
数を正しく数えたり、思った通りの数の「○」を書くことができていたら、
具体的な「数の構成」が分からなくても、ペーパー課題に正答することができます。
こういった問題は、おそらく出題されませんが、
リンゴの数が、全部で「13個」となろうとも、「29個」となろうとも、
正しく数えることさえできれば、正解することができるのが、このステップ1の方法です。
ただし、これは、あくまでも答えがわからなくなった時の応急処置であり、
あるいは、解答後に時間が余った時の「みなおし(確かめ)」に使う考え方だとするのがよいでしょう。
せっかくなので、幼児期に「数の構成」の学習をするのであれば、もうひとつ上のレベルを目指していきましょう。
ステップ2:10までの数の構成は、即答できるように「暗記」する。
例題の「5の構成」であれば、
5は「1と4(4と1)」「2と3(3と2)」に分けることができます。
(あるいは、「0と5(5と0)」というのもあるでしょう。)
「10の構成」であれば、
10は「1と9(9と1)」「2と8(8と2)」「3と7(7と3)」「4と6(6と4)」「5と5」に分けることができます。
この全てのパターン、組み合わせを、
即答できるようにすることを目指しましょう。
最初は、「指を使って数える」などして考えてもよいです。
それを繰り返しやっていくことで、
数えたり、考えたりしなくても正解がわかるところまで、覚えていけるようにします。
あれ、これって、「覚えこみ」ではないですか?
数の構成を「暗記」しましょう、と言うと、
「それは、思考を排除する「覚えこみ」なのではないか」という疑問が湧く方もいらっしゃるかもしれません。
おっしゃるとおり、
これは、紛れもない「覚えこみ」です。
え?ただ覚えさせる「詰め込み学習」ではなく、考える学習が大事なのではないの?
と言うご意見が聞こえてきそうですが、
この「(少なくとも10までの)数の構成」については、就学前に暗記しておけることが望ましいです。
なぜならば、この「数の構成」は、
そのまま、就学後の算数における「足し算」「引き算」の計算に直結するからです。
先ほどの「5は、2と3に分けられる」という問題を考えるとき、
頭の中では「5−2=3」という計算をしているのと同じ数の操作をしていることになります。
つまり、「数の構成」の問題に強くなるということは、
そのまま、就学後の計算学習の土台を作ることにもつながるのです。
ちなみに、こうした計算(四則演算)については、
「思考」というよりもむしろ「作業」であると考えることができます。
計算には「工夫する」という発想も必要ですが、それはまた別の話で、
基本的な計算力というのは、算数力を高める上での必要条件です。
(もちろん、「計算力」=「算数力」ではないことにも注意が必要です。計算練習だけで「算数が得意になった」と考えていると、後になって、算数学習の「忘れ物」を取りにもどる必要が出てきます。)
(ですから、こうした計算練習に関しては、それだけで「やり切った」感覚になるほどやりすぎない、というのもまた大切なことです。あくまでも、たくさんあるお勉強の中の「一部」でしかない、というバランス感覚も重要です。)
ステップ3:18までの数を、同様に即答できるようにする。
10までの数の構成が理解できたら、
11、12、…と数を増やしていって、
18までの数が、いくつといくつに分かれるかを、即座に答えられるようになることを目指しましょう。
(これは、小学校受験、というよりも、就学前準備という要素が濃くなりますので、本格的にやるのは暮れから年明け以降でもよいです。ただし、せっかくこのブログをご覧いただいている読者の皆様には、「年度末(=卒園時)には18までの数の構成を完成させる」ことを目標としてご設定いただければなと思っています。)
ご自宅でもできる「合わせて○にするゲーム」
数の構成の理解を進めるためには、
「合わせて○にするゲーム」がおすすめです。
例えば、「合わせて5にするゲーム」であれば、
出題者が、0〜5までの任意の数を言って、
解答者が、その数と合わせて5になる数を答える、というルールになります。
つまり、
「4」→「1」
「2」→「3」
「5」→「0」
といったふうに取り組みます。
ルールを変えて「合わせて7にするゲーム」「合わせて10にするゲーム」などとしていけば、
どんどん、数の構成の学習につなげることができます。
登降園時や、入浴時など、
いつでも取り組めるゲームです。
レベルが上がると、
出題者が、2つの数を言って、解答者が、その2つの数と合わせて○になる数を答えるルールで取り組むこともできるようになります。
例えば「合わせて10にするゲーム」として、
「1、5」→「4」
「3、6」→「1」
「6、4」→「0」
などと、先に言われた数の合成(足し算)をした上で、残りの数を考える、ということも、できるようになります。
これは、10−(1+5)=?という計算をしていることと等しいです。
ややこしそうに見えますが、ひとつの数を聞いて、答えが即答できるようになったら、取り組んでみてもよいでしょう。
大切なのは「ゲーム感覚」で取り組むことです。
机に向かって、ゴリゴリ計算練習をすることは、悪いことではありません。
(むしろ、就学後はそうした学習もどんどん取り組んでいくことになります。)
ただし、慣れないうちから「お勉強」然とした計算練習に取り組むことが、
習慣化させる上でのひとつの障壁になることがあります。
まずは、遊び感覚からでも、数の構成について触れていって、
時間がかかっても、正解できたら喜んでいけるような形式で、数のお勉強に取り組んでみてください。
次回引き続き、
「数の構成」をテーマに、算数学習ともつながる大切な視点についてまとめていきます。
お申し込み受付中の講座
金生先生の行動観察講座
対象:年長の皆様
日時:9月10日(土) ・10月8日(土) ・11月12日(土) ①8:30〜10:00 ②10:30〜12:00
受講料:各回10,000円(税込)
講師:金生先生
会場:四ツ谷教室
お申し込みは
金生先生の行動観察講座のお申し込みページより、必要事項をご入力の上、お申込みください。
提携教室
2歳から始める幼児教育
CROIRE(クロワール)幼児教室
ホームページは、→→→こちらをご覧ください(外部ページにリンクします)。
CROIRE(クロワール)幼児教室のブログは、→→→こちらです(外部ページにリンクします)。




