小学校受験の後の学習にもつながる「図形系列」

寒い日が続いています。

そんな中でも、子どもたちの笑顔に触れると、

芯から、温かくなりますね。

お子さまたちとご一緒に、お勉強させていただけることに、あらためて感謝です。

本日は、幼稚園でも取り組んだ「図形系列」の問題について紹介します。

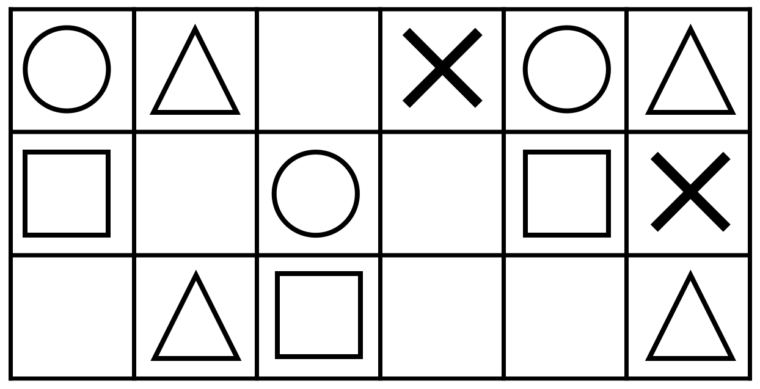
問）順番通りに形が並んでいます。上のマス目の、空いているお部屋に入る形を答えてください。

これだけを、いきなり出されると、なかなか難しい課題です。

大人でも、一瞬、考えてしまうかもしれませんが、

順番に、繰り返される形「○△□×」を、理解することができると、

たちどころに、答えがイメージできるようになります。

図形系列の学習は、この繰り返される形のリズムを口ずさみながら、空欄に入る形を考えるところから始まります。

「まーる、さんかく、しかくバツ、」

そうすると、多くの場合、次の空欄に入る形が理解できるようになります。

ここで大切なのは、「実際に、口に出してみる」ということです。

もちろん、小学校受験のペーパー課題の本番では、声を出しながら解くことはできません。

ですが、学びはじめにおいては、「声に出してみる」ことで、正解のイメージを、明確に持つことができます。

最初は、「○△□×」という、決められた順番をあらかじめ伝えてから、そのリズムを一緒に口ずさんでみても良いですし、

なれてきたら、

「どんな順番になっているかな」

と、お子さまに考えて、答えてもらうようにしてみてください。

この「図形系列」の法則性や順序をイメージできるようになると、

小学校以降での「数列」の学習にも、つながっていきます。

たとえば、

1,2,3,4,1,2,3,4,1,2,……

と続く数列の、

①50番目はどの数字ですか？

②25番目までの数字を全て足すと、いくつになりますか？

といった問題に対して、

｜1,2,3,4,｜1,2,3,4,｜1,2,……

と「1,2,3,4」のかたまりを意識して、解いていきます。

(完全に余談ですが、

①は、50÷４=12あまり2で、13番目のかたまりの2つ目なので、「２」が正解、

②は、25÷4=6あまり１で、6番目までのかたまりの和1+2+3+4=10で10×6=60に25番目の数１を足して「61」が正解です。)

小学校受験期の学習は、

小学校受験の後にも、繋がるような「考え方の土台」を育むこともできるのです。

逆に言えば、お子さまにとっては難しいものもあるでしょうから、

お子さまの理解力に合わせて、ヒントを与えながら、楽しく取り組んでみてください。